Метод Монте-Карло

Метод Монте-Карло и его точность

Под метдом Монте-Карло понимается численный метод решения
математических задач при помощи моделирования случайных величин.

Метод имеет две основных особенности. Первая — простая структура вычислительного алгоритма. Вторая — ошибка вычислений, как правило, пропорциональна √D૬／N
, где D — некоторая постоянная, а N — число испытаний. Ясно, что добиться высокой точности на таком пути невозможно. Поэтому обычно говорят, что метод Монте-Карло особенно эффективен при решении тех задач, в которых результат нужен с небольшой точностью.

Точность вычислений

В этом пункте хотелось бы указать важность именно второго параметра b. Лучше всего это показать на примере. Рассмотрим вычисление определенного интеграла.

Вычисление определенного интеграла эквивалентно вычислению площадей, что дает интуитивно понятный алгоритм вычисления интеграла. Я рассмотрю более эффективный метод. Однако не все знают, что вместо равномерно распределенной случайной величины в этом методе можно использовать практически любую случайную величину, заданную на том же интервале.

Итак, требуется вычислить определенный интеграл:

I=ഽg(x)dx

Выберем произвольную случайную величину ૬  с плотностью распределения p૬(x) , определенной на интервале(a,b) . И рассмотрим случайную величинуς=g(૬)/p૬(૬).

Математическое ожидание последней случайной величины равно:

Mς=ഽ[g(x)/p૬(x)]p૬(x)dx

Таким образом, получаем:

P(|1/NΣςi-I|≤3√D૬/N)≈0,9973

Последнее соотношение означает, что если выбрать N значений ૬1, ૬2 . . . ૬n, то при достаточно большом N:

1/NΣg(૬i)/p૬(૬i)≈I

.

Таким образом, для вычисления интеграла, можно использовать практически любую случайную величину ૬. Но дисперсия Dς, а вместе с ней и оценка точности, зависит от того какую случайную величину ૬ взять для проведения расчетов.

Можно показать, что Dς будет иметь минимальное значение, когда p૬(x) пропорционально |g(x)|. Выбрать такое значение p૬(x) в общем случае очень сложно (сложность эквивалентна сложности решаемой задачи), но руководствоваться этим соображением стоит, т.е. выбирать распределение вероятностей по форме схожее с модулем интегрируемой функции.

Численный пример

Теория, конечно, дело хорошее, но давайте рассмотрим численный пример: a=0; b=π/2; g(x)=cos(x) .
Вычислим значение интеграла с применением двух различных случайных величин.
В первом случае будем использовать равномерно распределенную случайную величину на [a,b], т.е. p૬(x)=2/π.
Во втором случае возьмем случайную величину с линейной плотностью на [a,b], т.е. p૬(x)=4/π(1-2x/π).

Вот график, указанных функций



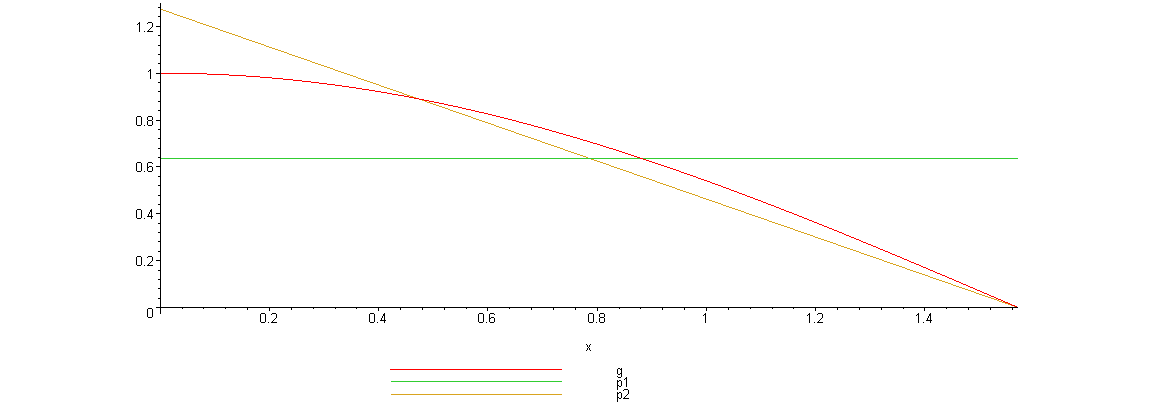
Нетрудно видеть, что линейная плотность лучше соответствует функции g(x).
Точное значение интеграла легко вычислить аналитически, оно равно 1.
Результаты одного моделирования при N=10:
Для равномерно распределенной случайной величины: I≈1,21666.
Для случайной величины с линейной плотностью распределения: I≈0,97641.
В первом случае относительная погрешность более 21%, а во втором 2.35%. Точность 3√Dς/N в первом случае равна 0.459, а во втором – 0.123.
Думаю, данный модельный пример показывает важность выбора случайной величины в методе Монте-Карло. Выбрав, правильную случайную величину, можно получить более высокую точность вычислений, при меньшем числе итераций.