Моделирование физических процессов

Моделирование физических процессов

Физика — наука, в которой математическое моделирование является чрезвычайно важным методом исследования. Сегодня уверенно выделяется третий фундаментальный раздел — вычислительная физика. Из многих конкретных причин выделим две наиболее часто встречающиеся: нелинейность многих физических процессов и необходимость исследования совместного движения многих тел, для которого приходится решать системы большого числа уравнений. Часто численное моделирование в физике называют вычислительным экспериментом, поскольку оно имеет много общего с лабораторным экспериментом.

Таблица 1

Аналогии между лабораторным и вычислительным экспериментами

Лабораторный эксперимент	Вычислительный эксперимент
Образец Физический прибор Калибровка прибора Измерение Анализ данных	Модель Программа для компьютера Тестирование программы Расчет Анализ данных

Численное моделирование (как и лабораторные эксперименты) чаще всего является инструментом познания качественных закономерностей природы. Важнейшим его этапом, когда расчеты уже завершены, является осознание результатов, представление их в максимально наглядной и удобной для восприятия форме. Забить числами экран компьютера или получить распечатку тех же чисел не означает закончить моделирование (даже если числа эти верны). Тут на помощь приходит другая замечательная особенность компьютера, дополняющая способность к быстрому счету — возможность визуализации абстракций. Представление результатов в виде графиков, диаграмм, траекторий движения динамических объектов в силу особенностей человеческого восприятия обогащает исследователя качественной информацией.

Второй закон динамики. В рассматриваемых ниже физических задачах фундаментальную роль играет второй закон динамики. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько, то равнодействующей, т.е. векторной сумме сил) и обратно пропорционально его массе: .

Чтобы исследовать ситуации, когда сила или масса не являются величинами постоянными, необходимо записать этот закон в более общей математической форме.

Допустим, что сила или масса (или и то, и другое) непостоянны и заданным образом зависят от времени, скорости движения или перемещения:   и . Достаточно наличия хотя бы одной из указанных зависимостей, чтобы ускорение было величиной переменной. В этом случае приведенная выше формула определяет его значение в тот момент времени, которому соответствуют сила и масса. Реальный интерес представляет временная зависимость перемещения  и скорости . Поскольку ускорение есть приращение скорости, а скорость — приращение перемещения, то

                                                    (1)

а сам второй закон динамики приобретает вид

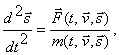                                                         (2)

или, что то же самое,

.                                                 (3)

Еще раз подчеркнем, что совсем необязательно, чтобы сила и/или масса зависели каждая от трех указанных переменных. Чаще всего в конкретных задачах присутствует в явном виде одна из указанных зависимостей.

Произведем дискретизацию по времени простейшим возможным способом. Если в некоторый момент времени  t_o  величина  s  имеет значение  s_o,  а величина   — значение , то в некоторый последующий момент времени будем иметь

                     (4)

Здесь индекс «0» означает величины в начальный момент времени.

При вычислениях значений  и  в последующие моменты времени можно поступать аналогично (4). Так, если известны значения    и    в момент , то

                                            (5)

Вопрос о выборе конкретного значения  весьма непрост и определяется следующими соображениями. При компьютерном моделировании можно получить решение задачи о движении тела на некотором конечном отрезке времени . Чем больше величина , тем:

а) меньше вычислений требуется для того, чтобы пройти весь заданный временной интервал;

б) меньшая точность в передаче значений непрерывных функций  и   их дискретными представлениями — наборами чисел   и .

Вопрос о точности результатов является в описываемом моделировании одним из центральных. Он распадается на два: как оценить эту точность и можно ли, уменьшая , достигать все большей точности?

Остановимся вначале на первом. Формулы (4), (5) представляют собой применение метода Эйлера для приближенного решения системы дифференциальных уравнений (3). Наиболее приемлемой при использовании этого и родственного ему методов (например, Рунге — Кутты) является эмпирическая оценка точности. Для этого отрезок  проходится с некоторым шагом , а затем с существенно меньшим (например, в два раза) шагом. Сравнение результатов в точках  t1, t2, ..., T позволяет составить представление о реальной точности результатов. Если она недостаточна, то следует повторить процесс с еще меньшим шагом.

Однако уменьшение шага  не всегда ведет к улучшению результатов моделирования. Одна из причин заключается в том, что чем меньше шаг, тем больше арифметических действий, ведущих к увеличению глобальной погрешности округления, другая причина глубже и связана со способом дискретизации — перехода от описания реально непрерывного процесса движения тел к описанию по простейшим формулам (4), (5). Обе причины могут привести к неустойчивости решения, т. е. к получению результатов, не имеющих реально ничего общего с истинными. Обычно неустойчивость становится заметной при повторениях процесса с уменьшением шага .

Более эффективными при моделировании процессов, описываемых дифференциальными уравнениями являются методы Рунге — Кутты более высокого порядка аппроксимации, чем метод Эйлера, неявные методы, методы типа "предиктор — корректор", отличающиеся повышенной устойчивостью, и другие, описанные в специальной литературе.

Конкретные физические модели

Движение тела, брошенного под углом к горизонту

Дифференциальные уравнения модели получаются из второго закона динамики проецированием скорости и перемещения на горизонтальную и вертикальную оси координат:

                                                         

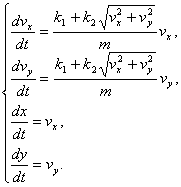
Входные параметры модели:

• m — масса тела;

• v — начальная скорость;

• a — угол начального наклона вектора скорости к горизонту;

• величины, определяющие коэффициенты сопротивления среды k₁ и k₂.